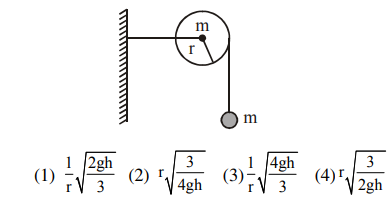
Sphere disc and ring are allowed to roll down on an inclined plane from its top, then order in which they reach at the bottom will be:
When a sphere, disc, and ring roll down an inclined plane, the key factor that determines how fast they reach the bottom is how their energy is distributed between rotational energy (spinning) and translational energy (moving forward). And it depends on their moment of inertia (how their mass is distributed).

Key Concept:

Rule:
Objects with less moment of inertia roll faster because they waste less energy in rotation.
Why Does Moment of Inertia Matter?
When rolling, part of the gravitational potential energy is used for spinning the object. Objects with higher moment of inertia use more energy for rotation, leaving less energy for moving forward. This makes them slower.
Order of Reaching the Bottom:
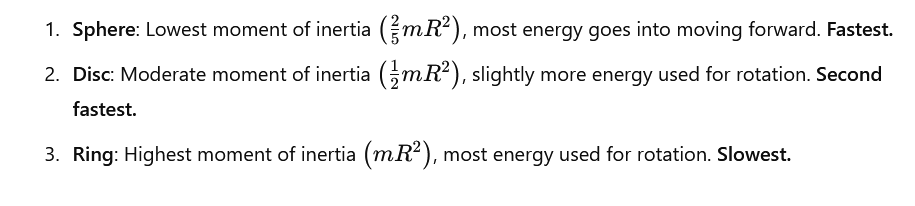
Final Intuition:
Imagine you’re pushing a big solid ball (like a bowling ball), a disc (like a coin), and a ring (like a hula hoop). The ball rolls easiest because its mass is more concentrated near the center. The ring takes the most effort because its mass is far from the center. This same principle applies here!