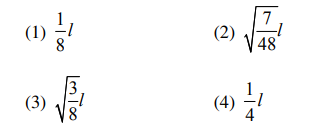a bob of mass mm is tied by a massless string whose other end is wound on a flywheel (disc) of radius rr and mass mm

As shown in the figure, a bob of mass mm is tied by a massless string whose other end is wound on a flywheel (disc) of radius rr and mass mm. When released from rest, the bob starts falling vertically. When it has covered a distance hh, what will be the angular speed of the wheel?

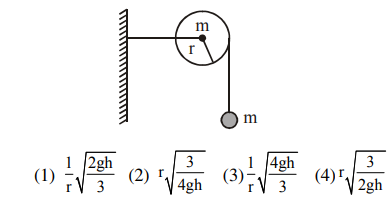
Solution:

Step 1: Energy Conservation

The total mechanical energy remains conserved as there is no energy loss due to non-conservative forces (like friction).

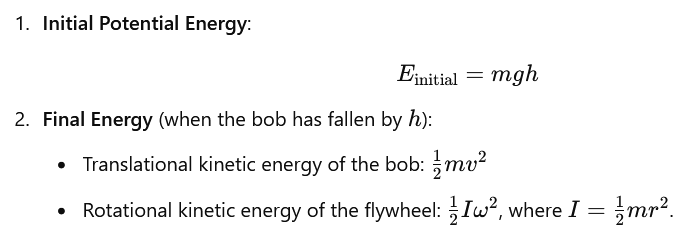
Step 2: Relating Linear and Angular Velocities

The bob and the flywheel are connected via a string. So, the linear velocity of the bob, vvv, is related to the angular velocity of the wheel, ω\omegaω, by:

v=rω

Step 3: Energy Conservation Equation

The total energy equation is:

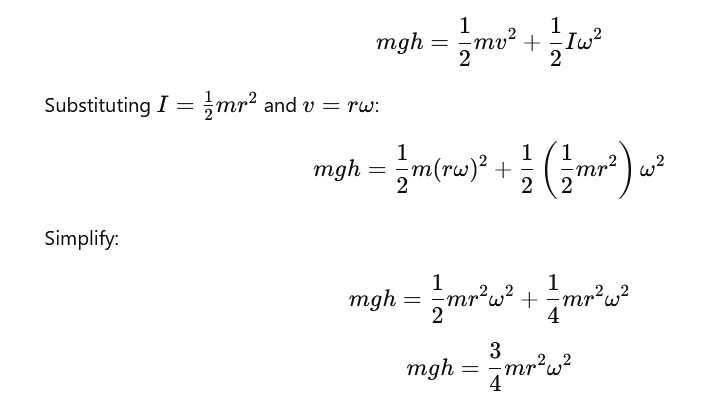
Step 4: Solve for ω

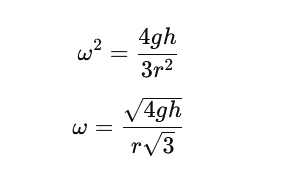
Conclusion:

This question beautifully illustrates the interplay of translational and rotational mechanics. By understanding energy conservation and the relationship between linear and angular velocities, you can solve such problems with ease.

For more such physics insights and exam preparation tips, stay tuned!