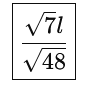The radius of gyration of a uniform rod of length l about an axis passing through a point at a distance l/4 from the center of the rod and perpendicular to it, is:
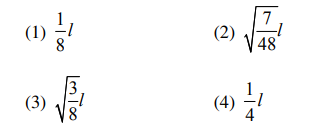
Solution Breakdown
We calculate the radius of gyration kkk using the formula:
I=Mk^2
Step 1: Find the Moment of Inertia Using the Parallel Axis Theorem

Step 2: Determine the Radius of Gyration k
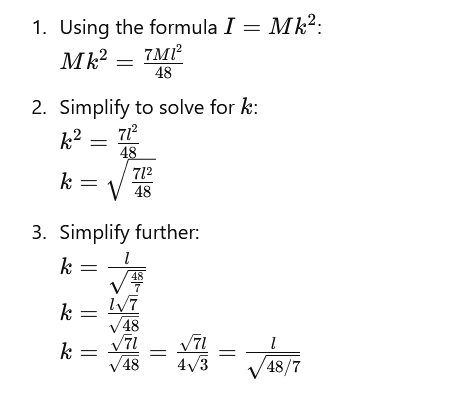
Final Answer
Thus, the radius of gyration is: